汉诺塔攻略怎么玩？

诺塔是一款经典的益智游戏,其玩法看似简单，实则蕴含着深刻的数学原理和策略思考，作为一名资深游戏玩家，我将带你深入了解汉诺塔的攻略与玩法，帮助你掌握这一挑战性十足的游戏。

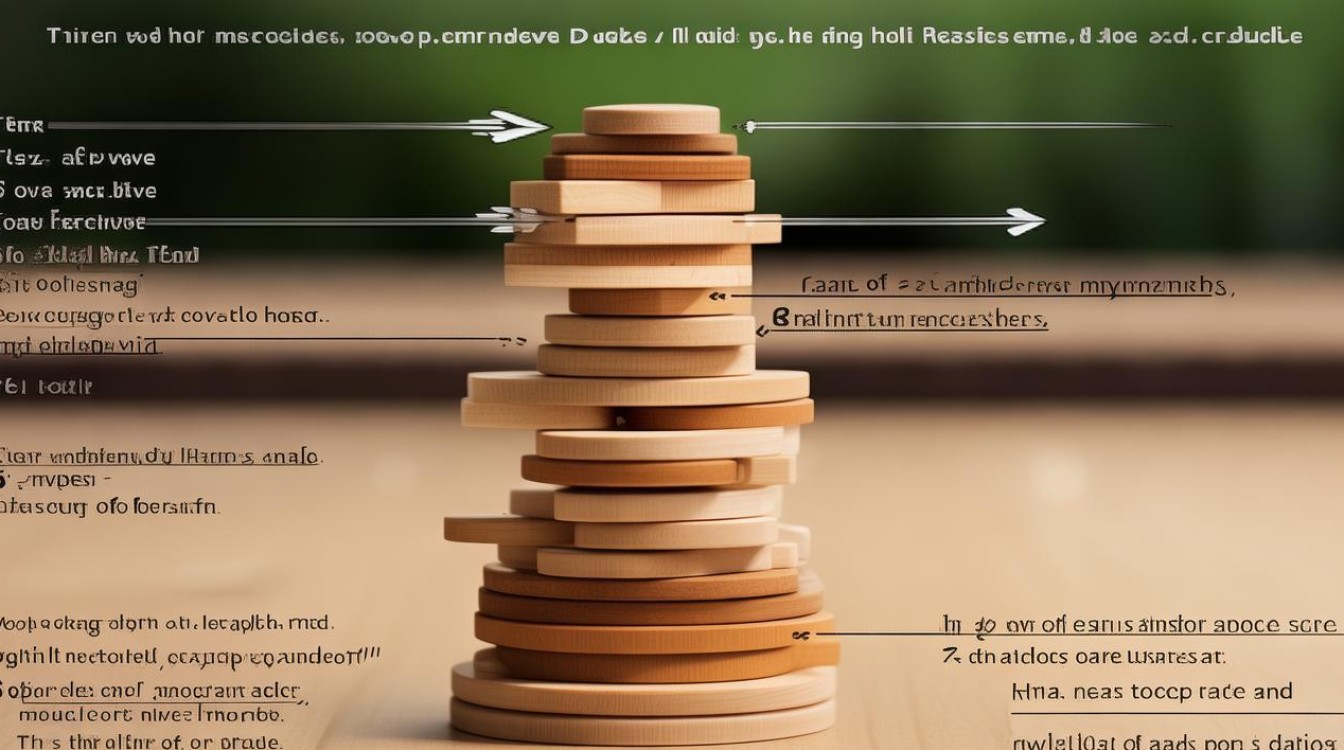
游戏规则与基础理解

汉诺塔游戏通常由三根柱子（A、B、C）和若干个大小不一的圆盘组成，初始时所有圆盘按从大到小的顺序叠放在柱子A上，游戏的目标是将所有圆盘从柱子A移动到柱子C上，同时遵循以下规则：

1. 每次只能移动一个圆盘：你不能同时拿起多个圆盘，必须逐个移动。
2. 大盘不能放在小盘上：任何时候，较大的圆盘都不能直接放在较小的圆盘上，只能放在空柱子或比它大的圆盘上。
3. 可利用辅助柱子：在移动过程中，你可以使用柱子B作为辅助，临时存放圆盘。

基本策略与递归思想

汉诺塔问题的解决依赖于递归的思想,假设你有N个圆盘，要将它们从柱子A移动到柱子C，可以分解为以下步骤：

1. 将前N-1个圆盘从A移动到B：这一步是递归的核心，你需要将除了最底下那个圆盘之外的所有圆盘移动到柱子B上，这同样需要遵循汉诺塔的规则。
2. 将第N个圆盘（最大的那个）从A移动到C：由于此时柱子C上没有圆盘（或者只有比这个圆盘更小的圆盘），你可以直接将它移动到目标位置。
3. 将前N-1个圆盘从B移动到C：再次使用递归，但这次的目标是将圆盘从B移动到C，同样可以利用柱子A作为辅助。

这个过程会一直递归下去,直到只剩下一个圆盘，这时你可以直接将其移动到目标柱子上。

具体操作步骤与技巧

虽然递归思想是解决汉诺塔问题的关键,但在实际游戏中，你可以采用一些具体的操作步骤和技巧来简化过程。

判断圆盘数量的奇偶性

• 如果圆盘数量是偶数：首先将最小的圆盘移动到中间的柱子（B）上。
• 如果圆盘数量是奇数：首先将最小的圆盘移动到最右边的柱子（C）上。

这一步是为了建立一个初始的“节奏”，便于后续的移动。

寻找连号圆盘

你需要找到当前柱子上连续编号的圆盘（比如1、2、3等），并计算它们的连号数目，这个步骤有助于你确定下一步应该移动哪个圆盘。

移动非连号圆盘中的最大者

根据连号数目,找到下一个应该移动的圆盘（通常是连号之后的那个最大圆盘），并将其移动到另一个柱子上，这个步骤是递归过程中的关键一步，它确保了你在移动过程中不会违反规则。

根据圆盘编号的奇偶性决定移动方向

• 如果移动的圆盘编号是奇数：将其移动到初始放置最小圆盘的柱子上。
• 如果移动的圆盘编号是偶数：将其移动到另一个柱子上（不是初始放置最小圆盘的柱子）。

这个规则确保了圆盘在移动过程中的有序性,避免了混乱。

重复上述步骤直至完成

继续按照上述步骤进行操作,直到所有圆盘都被移动到目标柱子上，在这个过程中，你需要保持耐心和冷静，不要因为一时的失误而破坏了整个计划。

实例演示

为了更好地理解上述策略,我们可以通过一个具体的例子来演示，假设我们有3个圆盘，分别标记为1（最小）、2、3（最大），初始时都放在柱子A上，我们的目标是将它们全部移动到柱子C上。

1. 初始状态：A(3,2,1) B() C()
2. 移动圆盘1到B：A(3,2) B(1) C() （因为3是奇数，所以先移到B）
3. 移动圆盘2到C：A(3) B(1) C(2) （将圆盘2直接移到目标柱C）
4. 移动圆盘1到C：A(3) B() C(2,1) （将圆盘1从B移到C）
5. 移动圆盘3到B：A() B(3) C(2,1) （将最大的圆盘3移到B）
6. 移动圆盘1到A：A(1) B(3) C(2) （将圆盘1从C移回A）
7. 移动圆盘2到B：A(1) B(3,2) C() （将圆盘2从C移到B）
8. 移动圆盘1到B：A() B(3,2,1) C() （最后将圆盘1从A移到B）

所有圆盘都按照规则从柱子A移动到了柱子B上,我们的目标是将所有圆盘移动到柱子C上，所以还需要再进行一轮类似的操作，但这个过程已经展示了汉诺塔移动的基本逻辑和策略。

归纳与心得

汉诺塔游戏不仅考验你的逻辑思维能力和耐心,还锻炼了你的递归思维和问题解决能力，通过不断实践和归纳经验，你会发现自己越来越擅长于这类需要策略和计划的游戏，不要急于求成，每一步都要谨慎考虑；也要保持冷静和耐心，相信自己的判断和决策，你才能在汉诺塔的世界里游刃有余，成为